ハイパーパラメータとは?
前回は様々なモデルで株価の予測を行いましたが、ハイパーパラメータは調整せず、ほぼデフォルトのまま使用していました。
ハイパーパラメータとは、学習前に決めておく必要があるパラメータです。端的に言えばモデルに与える引数のことで、前回アンサンブル学習で固定していたn_estimators=10などに相当します。
今回はちゃんとハイパーパラメータのチューニングを行い、その効果も確認してみたいと思います。
とにかくはじめます🍛
グリッドサーチ
まずはハイパーパラメータのチューニング方法として、もっともシンプルなグリッドサーチを使用します。
結果を見ればグリッドサーチが何をやっているかはわかると思うので、さっそくランダムフォレストを対象にチューニングしてみましょう。
ランダムフォレストにはいくつかパラメータがありますが、ここでは前回の記事でも出てきた以下2つのパラメータを対象とします
| パラメータ | 意味 | 探索範囲 |
|---|---|---|
| n_estimators | 木の数(前回記事では10固定) | [30, 50, 100, 200] |
| max_features | 弱学習器で使用する特徴量 | [6, 8, 10, 12, 20, 30] |
検証にはscikit-learnのGridSearchCVを使用します。
params = [
dict(n_estimators=[30, 50, 100, 200],
max_features=[6, 8, 10, 12, 20, 30])
]
search = GridSearchCV(RandomForestRegressor(),
params,
cv=5)
search.fit(x_train, y_train)
結果を図式します。 値が大きいほど優秀なモデルであり、一番大きい値は少しフォント大きくしておきました。

n_estimatorsは50、max_featuresは10が良いようで、木の数が多ければ良いというわけでは無いことが分かります。
グリッドサーチとはこのように、探索範囲の全組み合わせを総当たりで試しているだけです。
よって組み合わせの数で言えば、24通りということになります。
ベストなパラメータの精度は以下です。
| 対象 | RMSE | R2 |
|---|---|---|
| Train | 229.0(69.1) | 0.90(0.03) |
| Test | 200.1 | 0.90 |
ちなみに前回の結果(n_estimators=10、max_features=5)は以下ですから
| 対象 | RMSE | R2 |
|---|---|---|
| Train | 236.6(78.3) | 0.90(0.03) |
| Test | 227.3 | 0.87 |
確かにちょっと良くなりました。
ランダムサーチ
グリッドサーチの利点は分かりやすいことですが、欠点は効率が悪いことです。
ランダムフォレストには他にも多くのパラメータがあるのですが、 パラメータ数を増やすと探索範囲が爆発的に多くなってしまいます。
そこで今度はランダムサーチを試してみます。 これも結果を見れば何をやっているかは分かるので、さっそくやってみます。
パラメータは先ほどより増やして以下の5つです。
| パラメータ | 意味 | 探索範囲 |
|---|---|---|
| n_estimators | 木の数(前回記事では10固定) | randint(5, 300) |
| max_features | 弱学習器で使用する特徴量 | randint(1, 31) |
| max_depth | 木の深さ | [None, 3] |
| bootstrap | ブートストラップの有無 | [True, False] |
| criterion | 分割時の評価指標 | [‘mse’, ‘mae’] |
params = dict(
n_estimators=randint(5, 300),
max_features=randint(1, 31),
max_depth=[None, 3],
bootstrap=[True, False],
criterion=['mse', 'mae']
)
search = RandomizedSearchCV(RandomForestRegressor(), params,
cv=5,
n_iter=20)
search.fit(x_train, y_train)
探索結果としてn_estimatorsとmax_featuresの関係だけ図示すると…
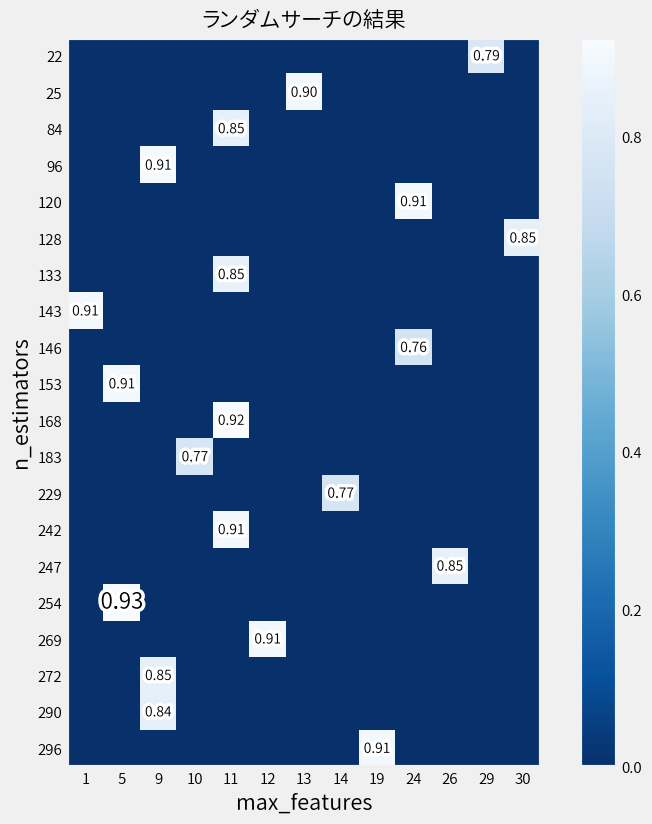
スコアがある場所のみが実際に計測されていることを意味しています。 つまりランダムサーチは探索空間の中をすべて試すのではなく、 ランダムにサンプリングされた組み合わせのみを対象とすることで探索範囲を絞ります。
上位5つの組み合わせは以下となりました。
| rank | score | bootstrap | criterion | max_depth | max_features | n_estimators |
|---|---|---|---|---|---|---|
| 1 | 0.925879 | False | mae | NaN | 5 | 254 |
| 2 | 0.924775 | False | mae | NaN | 11 | 168 |
| 3 | 0.914328 | True | mse | NaN | 9 | 96 |
| 4 | 0.911263 | False | mse | NaN | 11 | 242 |
| 5 | 0.910985 | False | mae | NaN | 19 | 296 |
今回のランダムサーチでは20通りの組み合わせしか試していないので、 グリッドサーチの全組み合わせ(24通り)を試すよりも探索時間も短くなっています。
にも関わらずベストスコアの組み合わせでの精度は、グリッドサーチより良くなりました。
| 対象 | RMSE | R2 |
|---|---|---|
| Train | 220.0(65.6) | 0.91(0.03) |
| Test | 154.1 | 0.94 |
ただしランダムにサンプリングするため、実行する度に最適な組み合わせは変わります。
例えば2回目はこんな結果でしたし。
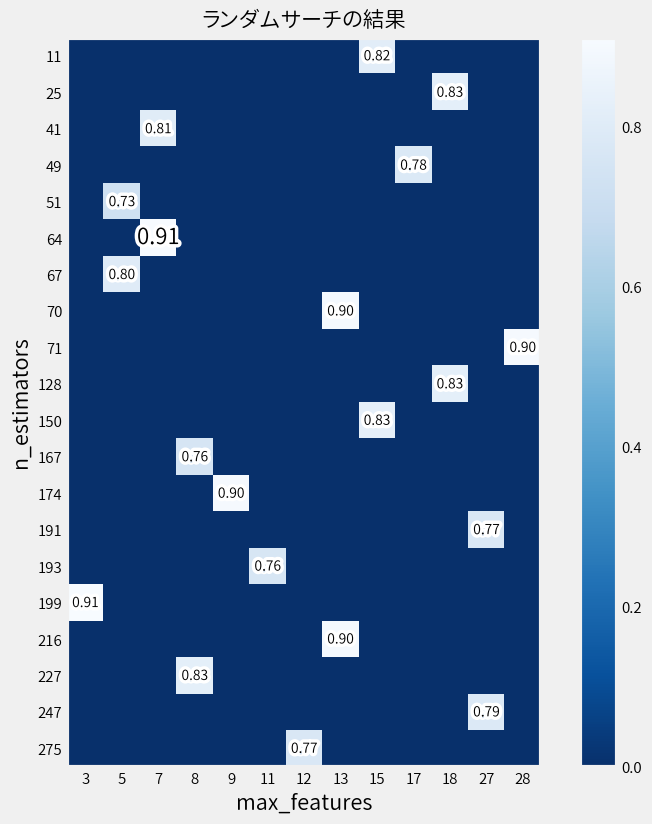
ベイズ最適化
ランダムサーチの欠点は必ずしも最適解に向かうわけでは無いので、どこで探索をやめるかの判断も難しいです。
そこで次にベイズ最適化を用いたチューニングを試してみます。 これにより精度がより良いと思われる組み合わせを積極的に試してくれることが期待できます。
さまざまな実装が存在しますがここでは
BayesSearchCV を使用します。
BayesSearchCVは、
GridSearchCVやRandomizedSearchCVと同じインタフェースなので違和感なく使えます。
param_grid = dict(
n_estimators=Integer(5, 300),
max_features=Integer(1, 31),
max_depth=Categorical([None, 3]),
bootstrap=Categorical([True, False]),
criterion=Categorical(['mse', 'mae'])
)
search = BayesSearchCV(RandomForestRegressor(), params,
cv=5,
n_iter=20)
search.fit(x_train, y_train)
最終的な精度はランダムサーチよりも良くなりました。
| 対象 | RMSE | R2 |
|---|---|---|
| Train | 207.0(69.6) | 0.92(0.02) |
| Test | 147.1 | 0.95 |
ランダムサーチとの違い
試行毎のスコア(左図)と、これまでの施行の最高スコア(右図)が以下です。
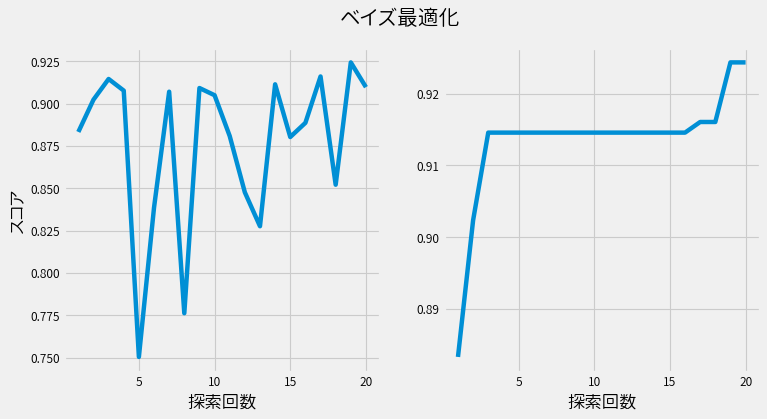
一方、ランダムサーチは以下です。
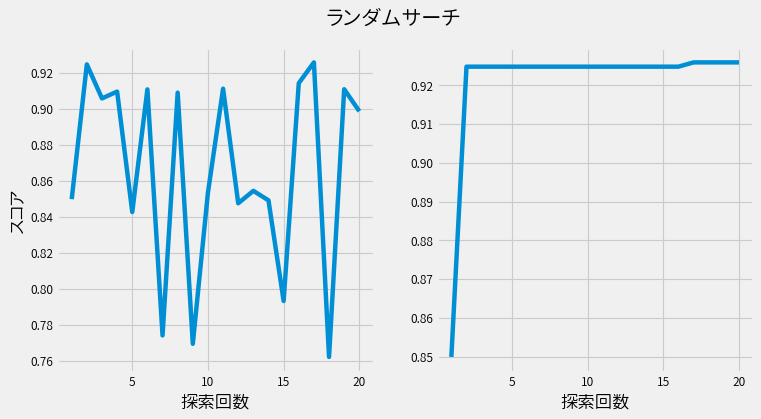
ランダムサーチに比べると、ベイズ最適化では各試行を重ねる度に、確実にスコアが上昇しているのが確認できます。 またスコアが上昇している間は、さらなる上昇を期待して探索を続けることが出来ます。
経験的な手法
経験的に確立されたチューニングの手順があるなら、 コンピュータに任せずに人が行った方が速いかもしれません。
例として以下リンクの手順で XGBoost の最適化を行います。 ちなみにXGBoostは前回も使用した勾配ブースティングを利用した実装の1つで、コンペでも高い評価を得られています。
Complete Guide to Parameter Tuning in XGBoost (with codes in Python)
- Fix learning rate and number of estimators for tuning tree-based parameters
- Tune max_depth and min_child_weight
- Tune gamma
- Tune subsample and colsample_bytree
- Tuning Regularization Parameters
- Reducing Learning Rate
結果だけ示すと、最終的に以下のパラメータが得られました。
model = xgb.XGBRegressor(
colsample_bytree=0.4,
gamma=0.1,
max_depth=13,
min_child_weight=3,
learning_rate=0.01,
reg_alpha=1E-5,
subsample=1.0,
n_estimators=1000,
scale_pos_weight=1,
)
精度は以下です。
| 対象 | RMSE | R2 |
|---|---|---|
| Train | 197.1(54.1) | 0.93(0.01) |
| Test | 170.0 | 0.93 |
悪い結果では無いですが、 随時結果を見ながらチューニングを行うので別に楽でも無いです。
ベイズ最適化との比較
上記の結果が良いのか調べるため、 XGBoostもベイズ最適化によりチューニングを行いました。
ここでは最適化の実装として hyperopt を使用します。
各パラメータ毎のスコアは以下となりました。 図からスコアが低くなるパラメータを中心に施行を繰り返していることもわかります。
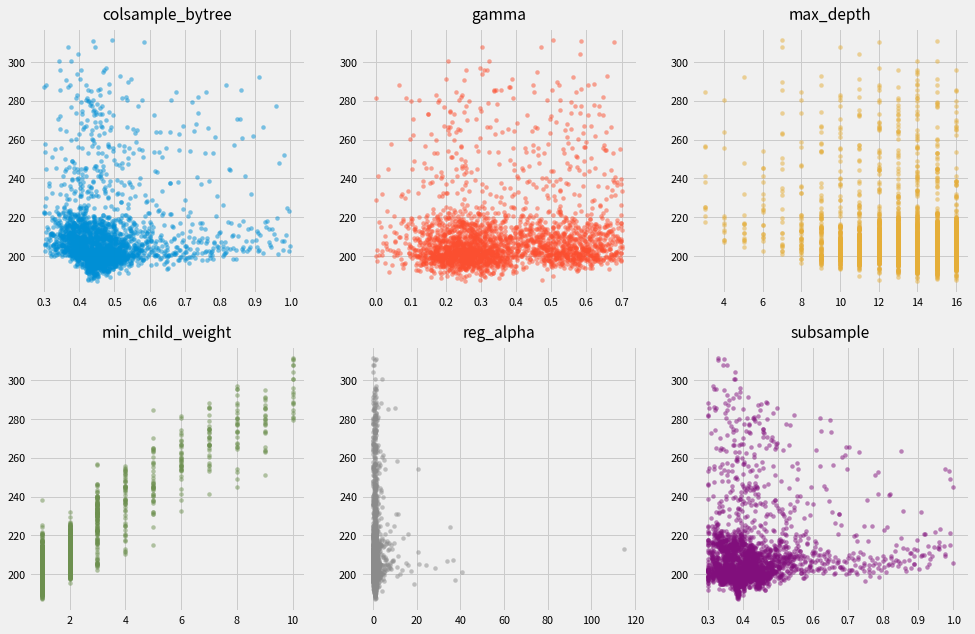
時間の都合でn_estimators=100固定にしているなど、
前提が違うので手動でチューニングした場合とは異なる結果になっています。
ただし精度は、手動チューニングと大差ありませんでした。
| 対象 | RMSE | R2 |
|---|---|---|
| Train | 183.1(48.3) | 0.94(0.01) |
| Test | 172.9 | 0.92 |
まとめ
パラメータチューニングにより精度の向上が確認できました。
問題はどのようにチューニングを行うかですが、 それは状況に応じて使い分けるという適当な結論でごまかしておきます。
なお結果的に、 今回チューニングを行ったXGBoostがここまでで最も良い精度となりました。 よって今回の株価予測には、XGBoostのモデルを採用することにします。
ちなみに今回使用していないくせになんですが、最近では optuna でチューニングしています。